Continuamos donde lo dejamos en la entrada anterior, en la que veíamos como medir la posición angular de un balancín dotado de un acelerómetro y un giroscopio. Una de las aplicaciones prácticas más directas será el control de un cuadricóptero, o en general cualquier aeromodelo.
Vamos a construir el modelo con una estructura en forma de cruz de aluminio, con la electrónica en el centro y «de momento» un motor con su variador de velocidad en uno de los extremos. Luego lo colgamos de un caballete y ya tenemos el balancín que describíamos en la anterior entrega.
Aunque la implementación del cálculo de la posición angular del balancín que usabamos en el primer capítulo era bastantes precisa y funcionaba bien al mover el balancín con la mano, al meter un motor en la ecuación la vibración aumenta notablemente y las medidas del acelerómetro tienen tanto ruido que sólo nos podemos fiar del giroscopio, pero este sin la referencia absoluta del acelerómetro empieza a acusar el efecto de la deriva al cabo de no mucho tiempo.
La solución se llama filtro de Kalman (aunque hay otras alternativas, esta es una de las más simples) y podemos encontrar un ejemplo muy sencillo en este foro.
Lo que hace el filtro es reducir el ruido casi a cero, a la vez que elimina la deriva del giroscopio. Ajustando los parámetros R_angle,Q_angle y Q_gyro se consigue reducir el ruido sin aumentar mucho el tiempo de respuesta.
Ahora tenemos una estimación fiable de la posición en la variable «angulo«.
Tomamos el valor del canal 6 de la emisora para calcular un ángulo de referencia que será la posición deseada en el balancín así como el estado del interruptor del canal 5 para corta la potencia del motor en caso de «emergencia».
Utilizaré un PID para calcular la potencia necesaria en el motor. El PID tiene tres componentes:
- Kp es el término proporcional. La ganancia que se aplica al error de posición para calcular la potencia del motor. Ganancias altas reducen el error a costa de aumentar la inestabilidad del sistema.
- Ki es el término de control integral que se aplica sobre la integral del error (en un sistema continuo), como trabajamos en un sistema discreto (muestreado) la integral se aproxima por la suma de errores pasados multiplicado por el periodo de muestreo. Se usa para reducir a 0 el error estacionario del sistema.
- Kd es el término derivativo, que se aplica sobre la variación del error. Sólo afecta a la potencia cuando el error está cambiando, de forma que «limita» la velocidad a la que se reduce el error impidiendo que el sistema se vuelva inestable y reduciendo el sobrepaso excesivo de la referencia. Tiene como inconveniente que amplifica mucho el ruido, lo cual es un problema en un cuadricoptero que tiene una vibración muy alta.
- En la práctica he sustituido el valor Kd del PID por otro mucho más utilizable que he llamado Kgiro. En lugar de aplicarlo sobre la variación del error, utilizo la velocidad angular que me entrega el giroscopio. Para que tenga el mismo efecto que el término derivativo debe ser negativa (Si e es el error y A el ángulo: de/dt=dAref/dt-dA/dt cuando el ángulo de referencia es cte. la derivada se hace cero y por tanto dE/dt =-dA/dt que es precisamente el valor del giroscópio en negativo). Es muchísimo menos ruidosa que la derivada del error (que incluye los datos del acelerómetro) y por tanto se pude ajustar a valores mucho más altos sin sufrir el ruido.
Todos estos parámetros hay que «sintonizarlos» para que el error sea mínimo, el tiempo de reacción máximo y la estabilidad lo mayor posible, para hacerlo uno de los métodos más empleados es el de Ziegler-Nichols:
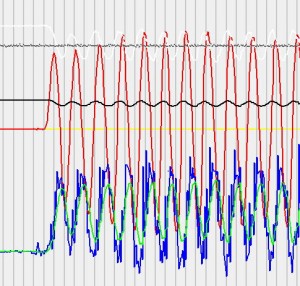
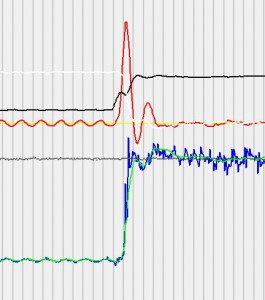
- Ponemos a cero la parte derivativa e integral y vamos aumentando la Kp hasta que el sistema responde a un cambio en la consigna de tipo «escalón» con una oscilación automantenida. Esa Kp es la que se conoce como ganancia crítica Kcr y el periodo de oscilación se denomina Pcr. La ganancia la pondremos como Kp=0.6*Kcr
- El tiempo integral Ti = 0.5*Pcr y la ganancia Ki es Ki=Kp/Ti
- El tiempo derivativo Td = 0.125*Pcr es igual a la ganancia derivativa que aplicamos al giroscopio multiplicada por -Kp.
Haciendo pruebas sobre el sistema he sacado el valor de Kcr=0.2 y Pcr=2.1 sg que proporciona los parámetros Kp=0.12 Ki=0.114 Kd=0.0315.
Sin embargo aunque el sistema es estable y tiene error cero en el estacionario, experimentalmente se ve que es demasiado lento. No he perdido el tiempo buscando el origen del problema, seguramente una mala identificación de los valores críticos, o que el sistema no es suficientemente lineal, en cualquier caso partiendo de estos valores, por prueba y error se llega a unos mucho mejores Kp=0.12 Ki=6 Kgiro=-0.8. Simplemente partimos de la ganancia que nos da Z-N y vamos aumentando la integral hasta que tenemos la velocidad de respuesta deseada, luego eliminamos las oscilaciones aumentando la parte derivativa (en este caso Kgiro).
Aquí os dejo el programa utilizado para hacer las pruebas:
Fichero sólo visible para usuarios registrados



1 ping
[…] « Control de un balancín II […]